Status for Mathematics students: List B for third years. If numbers permit second and fourth years may take this module as an unusual option, but confirmation will only be given at the start of Term 2.
Commitment: 10 two hour and10 one hour seminars (including some assessed problem solving)
Assessment: 10% from weekley seminars, 40% from assignment, 50% two hour exam in June
Prerequisites: None
Introduction
This module gives you the opportunity to engage in mathematical problem solving and to develop problem solving skills through reflecting on a set of heuristics. You will work both individually and in groups on mathematical problems, drawing out the strategies you use and comparing them with other approaches.
General aims
This module will enable you to develop your problem solving skills; use explicit strategies for beginning, working on and reflecting on mathematical problems; draw together mathematical and reasoning techniques to explore open ended problems; use and develop schema of heuristics for problem solving.
This module provides an underpinning for subsequent mathematical modules. It should provide you with the confidence to tackle unfamiliar problems, think through solutions and present rigorous and convincing arguments for your conjectures. While only small amounts of mathematical content will be used in this course which will extend directly into other courses, the skills developed should have wide ranging applicability.
Intended Outcomes
Learning objectives
The intended outcomes are that by the end of the module you should be able to:
- Use an explicit problem solving scheme to control your approach to mathematical problems
- Explain the role played by different phases of problem solving
- Critically evaluate your own problem solving practice
Organisation
The module runs in term 2, weeks 1-10
Thursday 14:00-15:00 OC0.04 (new teaching and learning building)
Friday 15:00-17:00 OC0.04
Most weeks the Thursday slot will be used for the weekly (assessed) problem session, but this will not be the case every week. You are expected to attend all three timetabled hours.
Assessment Details
- A flat 10% given for ‘serious attempts’ at problems during the course. Each week, you will be assigned a problem for the seminar. At then end of the seminar, you should present a ‘rubric’ of your work on that problem so far. If you submit at least 7 rubrics, deemed to be ‘serious attempts’, you will get 10%.
- One problem-solving assignment (40%) (deemed to be the equivalent of 2000 words) due by noon on Monday 20th March 2017 by electronic upload (pdf).
- A 2 hour examination in Summer Term 2017 (50%).
Topology is the study of properties of spaces that are invariant under continuous deformations. An often cited example is that a cup is topologically equivalent to a torus, but not to a sphere. In general, topology is the rigorous development of ideas related to concepts such “nearness”, “neighbourhood”, and “convergence”.
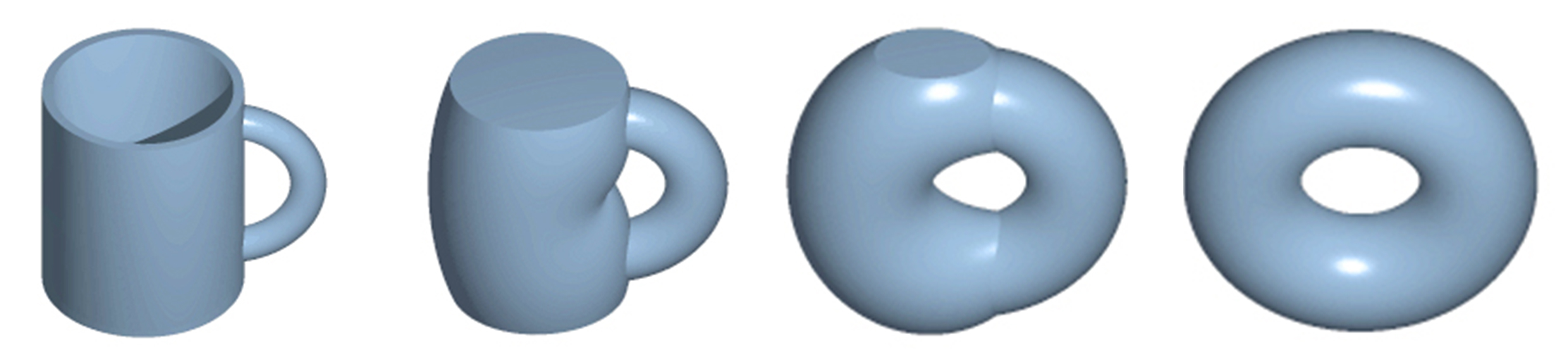
This module covers topological spaces and their properties, homotopy, the fundamental group, Galois correspondence, universal covers, free products, and CV complexes.
The course will follow largely the first chapter of
- Allen Hatcher. Algebraic Topology. Cambridge University Press.
An electronic version of the book is freely available on the author’s web page, and a printed version should be available in the library or the campus bookshop.
This module investigates how solutions to systems of ODEs (in particular) change as parameters are smoothly varied resulting in smooth changes to steady states (bifurcations), sudden changes (catastrophes) and how inherent symmetry in the system can also be exploited. The module will be application driven with suitable reference to the historical significance of the material in relation to the Mathematics Institute (chiefly through the work of Christopher Zeeman and later Ian Stewart). It will be most suitable for third year BSc. students with an interest in modelling and applications of mathematics to the real world relying only on core modules from previous years as prerequisites and concentrating more on the application of theories rather than rigorous proof.
Indicative content (precise details and order still being finalised):
1. Typical one-parameter bifurcations: transcritical, saddle-node, pitchfork bifurcations, Bogdanov-Takens, Hopf bifurcations leading to periodic solutions. Structural stability.
2. Motivating examples from catastrophe and equivariant bifurcation theories, for example Zeeman Catastrophe Machine, ship dynamics, deformations of an elastic cube, $D_4$-invariant functional.
3. Germs, equivalence of germs, unfoldings. The cusp catastrophe, examples including Spruce-Budworm, speciation, stock market, caustics. Thom’s 7 Elementary Catastrophes (largely through exposition rather than proof). Some discussion on the historical controversies.
4. Steady-State Bifurcations in symmetric systems, equivariance, Equivariant Branching Lemma, linear stability and applications including coupled cell networks and speciation.
5. Time Periocicity and Spatio-Temporal Symmetry: Animal gaits, characterization of possible spatio-temporal symmetries, rings of cells, coupled cell networks, H/K Theorem, Equivariant Hopf Theorem.
Further topics from (if time and interest):
Euclidean Equivariant systems (example of liquid crystals), bifurcation from group orbits (Taylor Couette), heteroclinic cycles, symmetric chaos, Reaction-Diffusion equations, networks of cells (groupoid formalism).
This module, MA4J7 (cohomology and Poincaré duality), has the prerequisites MA3F1 (introduction to topology) and MA3H6 (algebraic topology).
Cohomology is a dual theory to homology; it continues our development of algebraic tools for the study of topological spaces. Cohomology is a richer, more algebraic, theory than homology is because it has a naturally defined ring structure coming from the cup product. It is also a key tool in the modern proof of Poincaré duality for manifolds.
The material covered in this module is essentially required for advanced study in the fields of topology, differential geometry, algebraic geometry, algebraic number theory, and others.
Examinable topics from the module;
The first part concerning basics of Ising model in the extent covered in lectures
is close to Chapters 3.1-3.7 of the book Statistical Mechanics of Lattice systems
by S. Friedli and Y. Velenik
Including, in particular, following Statements with proofs:
Existence of the free energy (preassure) in the thermodynamic limit and its properties
Fekete’s Lemma
Correlation inequalities: GKS I, II, FKG
Existence of magnetizatin in the thermodynamic limit and its properties
Peierls argument
Analyticity of the free energy in d=1
Kramers-Wanier duality
Convergence of the abstract cluster expanion and its applications
High and Low temperature expansion
In the second part we followed chosen sections from the PCMI lecturea
by H. Duminil-Copin (major parts of Section 1 and 2)
In particular,
Definitions of order parameters and transition/critical temperatures.
Overview of proven and conjectured statement for Ising, Potts, and O models.
Coupling between random cluster (RC) a Potts models (Edwards-Sokal measure)
Equivalence of RC and Potts model order parameters.
The percolation transitiuon for random cluster models.
Sufficient condition for monotonicity for percolation models
Propositions for RC mofrls:
comparison between boundary conditions,
monotonicity,
FKG inequality
Existence of a sharp phase transitions for RC and Potts models
Burton-Kean theorem